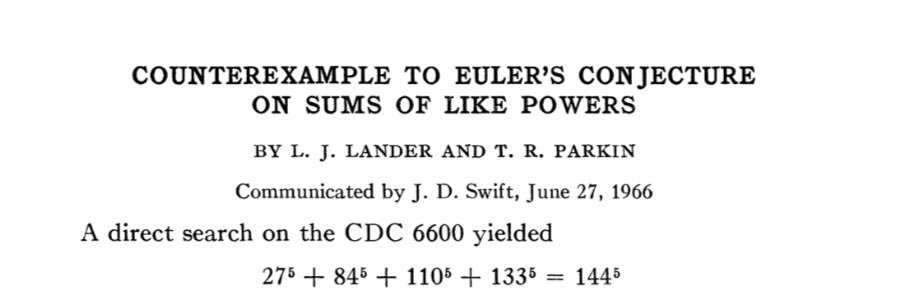オイラー予想

オイラー予想（オイラーよそう、Euler's sum of powers conjecture）とは、スイスの数学者レオンハルト・オイラーが提唱した、フェルマーの最終定理を発展させた数学的予想である。現在では、反例によってこの予想は偽である（正しくない）ことが証明されている。

予想の内容

オイラーはフェルマーの最終定理の n = 3 のとき、すなわち

x³ y³ = z³

を満たす自然数の解 (x, y, z) は存在しないことを証明した。 ここから、フェルマーの最終定理を拡張して、

x⁴ y⁴ z⁴ = w⁴

を満たす自然数の解 (x, y, z, w) は存在しない、と予想した。

同様に

x⁵ y⁵ z⁵ w⁵ = v⁵

x⁶ y⁶ z⁶ w⁶ v⁶ = u⁶

を満たす自然数の解も存在しない、とした。

すなわち、n > 3 とすると、n − 1 個の n 乗数の和を1個の n 乗数で表すことはできないということを示唆した。 これが、オイラー予想である。

歴史

オイラーの発表以降、比較的小さな自然数では反例を見つけることができず、長い間正しいと信じられてきた。

しかし1966年にレオン・J・ランダーとトーマス・R・パーキンによって n = 5 の場合の反例として解 (27, 84, 110, 133, 144) が発見され、27⁵ 84⁵ 110⁵ 133⁵ = 144⁵ が成り立つことが確認された。これには当時世界最速のスーパーコンピュータであったCDC 6600が用いられた。

この発見から n = 4 の場合も反例がある可能性があるとして研究が続けられ、1986年にハーバード大学のノーム・エルキーズ(Noam Elkies)が、楕円曲線論とコンピュータを用いて発見した。その反例は 2682440⁴ 15365639⁴ 18796760⁴ = 20615673⁴ という複雑なものだった。この発見と同時に解は無限に存在することも確認され、約200年間未解決となっていたオイラー予想は、否定的に解決された。

また、2004年にはジム・フライによってn=5の場合の反例85282⁵ 28969⁵ 3183⁵ 55⁵ = 85359⁵が発見された。

例

箇条書きされている式は、n − 1 個の n 乗数の和を1個の n 乗数で表すオイラー予想の反例である。 そうではない式は、n 個の n 乗数の和を1個の n 乗数で表すオイラー予想に従う例である。

k = 4

95800⁴ 217519⁴ 414560⁴ = 422481⁴ (R. Frye, 1988)

30⁴ 120⁴ 272⁴ 315⁴ = 353⁴ (R. Norrie, 1911)

（R. Norrie によって最小の解であることが示されている。）

k = 5

27⁵ 84⁵ 110⁵ 133⁵ = 144⁵ (Lander & Parkin, 1966)

19⁵ 43⁵ 46⁵ 47⁵ 67⁵ = 72⁵ (Lander, Parkin, Selfridge, smallest, 1967)

21⁵ 23⁵ 37⁵ 79⁵ 84⁵ = 94⁵ (Lander, Parkin, Selfridge, second smallest, 1967)

7⁵ 43⁵ 57⁵ 80⁵ 100⁵ = 107⁵ (Sastry, 1934, third smallest)

k = 7

127⁷ 258⁷ 266⁷ 413⁷ 430⁷ 439⁷ 525⁷ = 568⁷ (M. Dodrill, 1999)

k = 8

90⁸ 223⁸ 478⁸ 524⁸ 748⁸ 1088⁸ 1190⁸ 1324⁸ = 1409⁸ (S. Chase, 2000)

関連項目

• ランダー・パーキン・セルフリッジ予想

参考文献