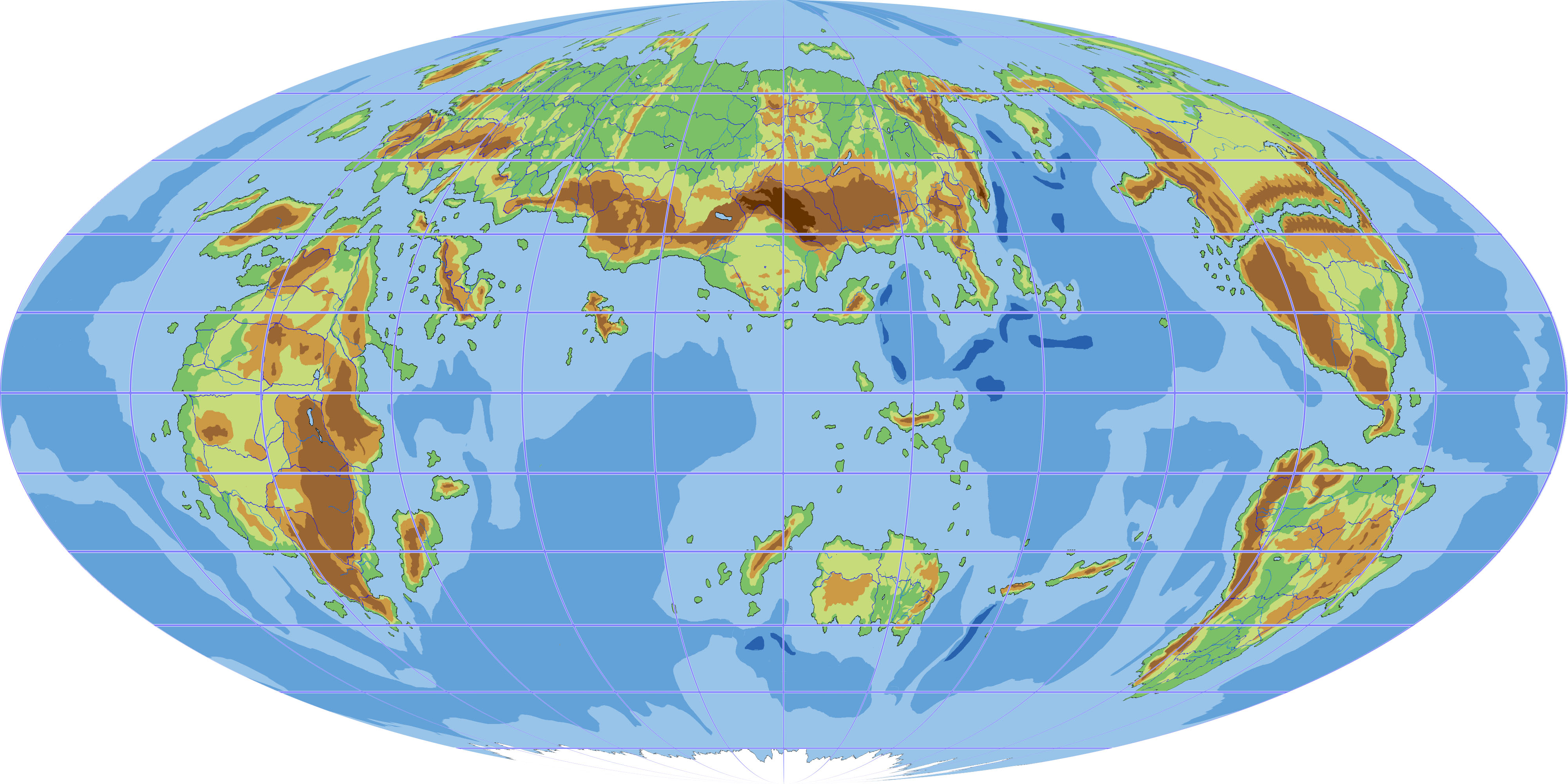
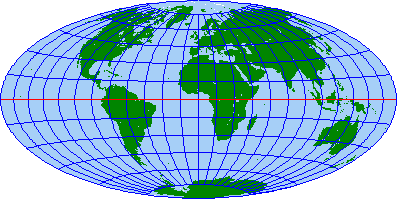
ハンメル図法

ハンメル図法（ハンメルずほう）とは、主に世界全図を描くために考案された地図投影法の一種である。正積な擬方位図法である。

1892年にエルンスト・ハンメルが考案した。1889年に考案されたエイトフ図法において正距方位図法を用いた部分を、ランベルト正積方位図法に置き換えて正積図法にしたものである。

赤道を基準とする場合、まず地球表面を経度方向1/2に「圧縮」して半球に収まるようにする。この半球に凝縮した地表をランベルト正積方位図法で描く。その地図を横方向2倍に引き伸ばす。この方法で描かれるのがハンメル図法である。

地図上のxとyの座標を緯度${\displaystyle \phi }$と経度${\displaystyle \lambda }$で表すと、以下のようになる。

${\displaystyle x={\frac {2{\sqrt {2}}\cos(\phi )\sin \left({\frac {\lambda }{2}}\right)}{\sqrt {1 \cos(\phi )\cos \left({\frac {\lambda }{2}}\right)}}}}$

${\displaystyle y={\frac {{\sqrt {2}}\sin(\phi )}{\sqrt {1 \cos(\phi )\cos \left({\frac {\lambda }{2}}\right)}}}}$

縦横比が1:2の楕円である正積図法という点でモルワイデ図法と似ているが、モルワイデ図法が全ての緯線を平行直線として描くのが大前提であるのに対し、ハンメル図法はそのようになっていない。モルワイデ図法は中心点の正角性が崩れている（縦方向に少し伸びている）という点で全ての図法の中でもやや特異だが、ハンメル図法の中心点は正角である。

「緯線が直線ではない」という点が気にならない場合、たとえばスピルハウス海洋図法のような斜軸法で使われることがある。

「経度方向に2分の1にしてランベルト正積方位図法で描いた後、横方向に2倍する」という操作の2という倍率を他の値に変えると、楕円形にはならないが似たような正積図法が得られる(エケルト・グライフェンドルフ図法)。

脚注